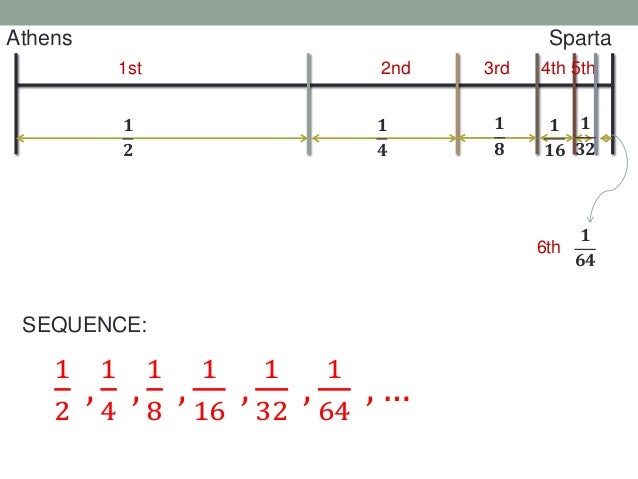
1 2 1 4 1 6 Sequence

1 2 2 1 2 1 4 4 1 4 1 6 6 1 6 1 8 8 1 8 a1 2 n 7 a7.

1 2 1 4 1 6 sequence. In the figure on the left if the large square is taken to have area 1 then the largest black square has area 1 2 1 2 1 4. For example 1 0 8 0 2 and 1 4 1 2 0 2. 2 1 2 2 2 3. Active 7 years 11 months ago.

In mathematics the infinite series 1 2 1 4 1 8 1 16 is an elementary example of a geometric series that converges absolutely. We can subtract a number of the sequence minus the number right before that number. Ask question asked 7 years 11 months ago. Now we must get the reciprocals of the terms to make them an arithmetic sequence.

Get an answer for for the series 1 2 1 4 1 6 1 8 1 10 1 12 1 14 1 16 what isthe nth term and find homework help for other math questions at enotes. Viewed 17k times 5. Another way to write it would be. 1 2 5 1 32 or alternatively by following the pattern from your already given series values.

There are many different expressions that can be shown to be equivalent to the problem such as the form. Sequences of numbers series and how to sum them section solvers solvers. What is the nth term of the harmonic sequence 1 2 1 4 1 6 1 8 log on algebra. So we have to add 0 2 from 1 6 to find the next term which is 1 8 then add 1 8 0 2 to get 2 as the number after that then add 2 0 2 2 2 to get the final number.

A7 a1 n 1 d a7 2 7 1 2 a7 2 12 a7 14 now just get. 1 16 1 2 1 32. The answer is simply evaluated by taking. Sequence sum 1 2 1 4 1 6 to infinite.

1 32 seems most likely. Algebra sequences and series solution. D a2 a1 4 2 2. Frac 1 2 frac 1 4 frac 1 6 ldots frac 1 2k ldots i can t get my head around how to prove this converges.

The series 1 4 1 16 1 64 1 256 lends itself to some particularly simple visual demonstrations because a square and a triangle both divide into four similar pieces each of which contains 1 4 the area of the original. Sum n 0 i 1 2 n in your question i 4 and you are asking for the value at i 5. 2 begingroup i ve been told the following series converges. This appears to be the geometric series 1 2 n starting at n 0.