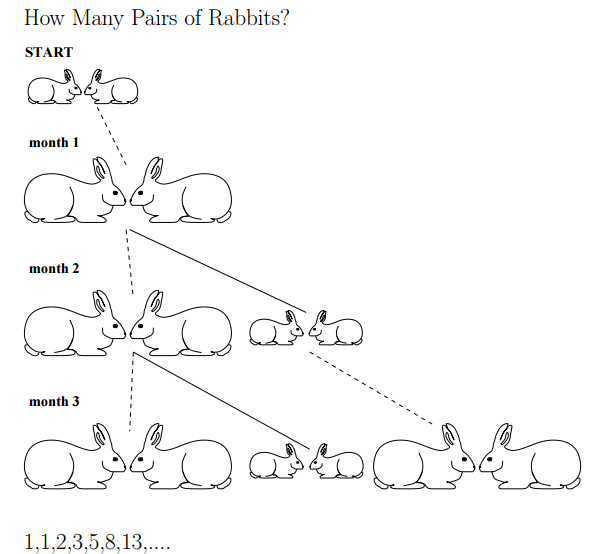
Fibonacci Sequence 1 1 2 3 5 8 Fibonacci Series In Nature Examples

The ratio between the numbers 1 618034 is frequently called the golden ratio or golden number.
Fibonacci sequence 1 1 2 3 5 8 fibonacci series in nature examples. Fibonacci sequence is a sequence of numbers where each number is the sum of the 2 previous numbers except the first two numbers that are 0 and 1. The fibonacci sequence is a sequence where the next term is the sum of the previous two terms. We ve talked about the fibonacci series and the golden ratio before but it s worth a quick review the fibonacci sequence starts like this. 1 1 2 3 5 8 13.
In a fibonacci sequence the next term is found by adding the previous two terms together. 0 1 1 2 3 5 8 13. F 1 1. We can observe that this implementation does a lot of repeated work see the following recursion tree.
1 1 2 3 5 8 13 21 34 55 89 144 and on to infinity. Golden ratio nature golden ratio and fibonacci numbers number patterns. This series of numbers is known as the fibonacci numbers or the fibonacci sequence. 1 1 2 3 5 8 13 in this example 1 and 1 are the first two terms.
Fibonacci day is november 23rd as it has the digits 1 1 2 3 which is part of the sequence. F 0 0. So next nov 23 let everyone know. The negative fibonacci sequence.
C code of fibonacci function. T n t n 1 t n 2 which is exponential. It is a natural occurrence that different things develop based upon the sequence. Everybody has heard of the fibonacci sequence and has at some point seen its stream of numbers.
1 1 2 3 5 8 13 and 21. So this is a bad implementation for nth fibonacci number. A tiling with squares whose side lengths are successive fibonacci numbers. The first two terms of the fibonacci sequence are 0 followed by 1.
In mathematics the fibonacci numbers commonly denoted f n form a sequence called the fibonacci sequence such that each number is the sum of the two preceding ones starting from 0 and 1. The fibonacci sequence is found all throughout nature too.




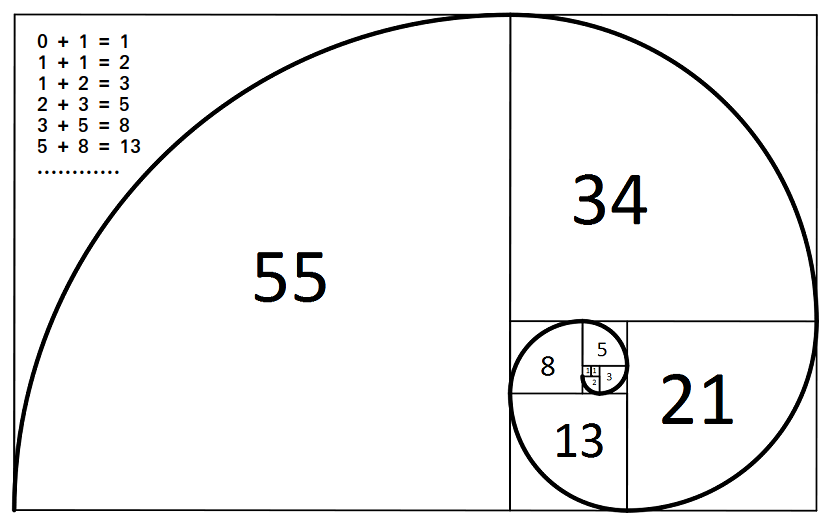

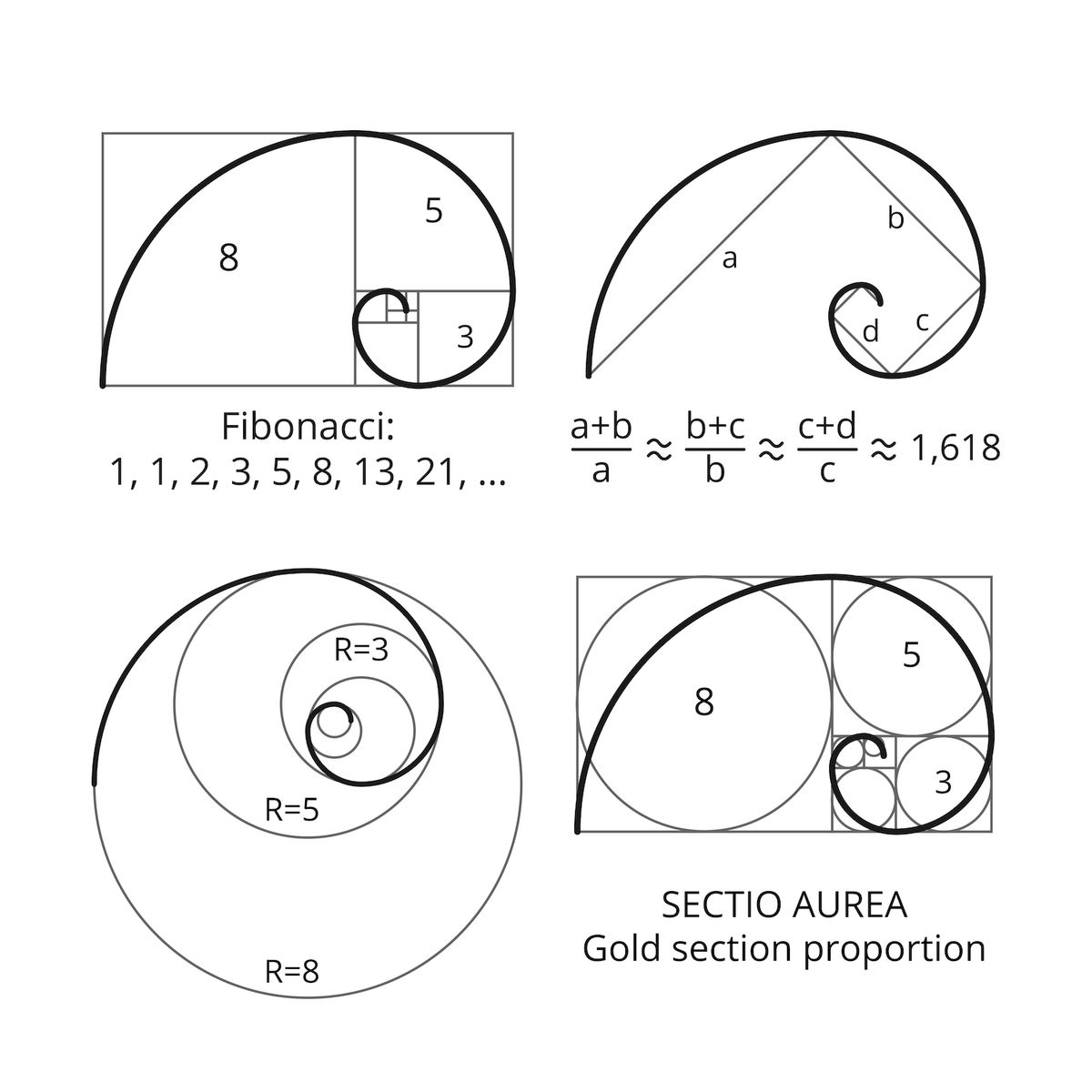





/https://public-media.si-cdn.com/filer/3a/70/3a70f58d-dabc-4d54-ba16-1d1548594720/2560px-fibonaccispiralsvg.jpg)